Frequency Analysis of Images and Diffusion Models: From Structure to Details

As someone interested in generative AI, I’ve been diving into why diffusion models produce such sharp and coherent images. One of the most insightful perspectives comes from frequency analysis: decomposing images into low-frequency (broad structure) and high-frequency (fine details) components using the Fourier transform.

This short post summarizes two key observations I made while experimenting:

Different image categories have distinct low/high-frequency energy profiles.
During the diffusion denoising process, the ratio of high-frequency to low-frequency energy steadily increases.

The goal is to provide a concise, intuitive bridge between frequency-domain thinking and how diffusion models work.

Frequency Components in Natural Images

Any image can be decomposed via the 2D Discrete Fourier Transform (DFT) into a spectrum where:

Low frequencies (near the center of the spectrum) capture global structure, large shapes, and broad color variations.
High frequencies (toward the edges) capture edges, textures, and fine details.

Scenery vs. Portraits

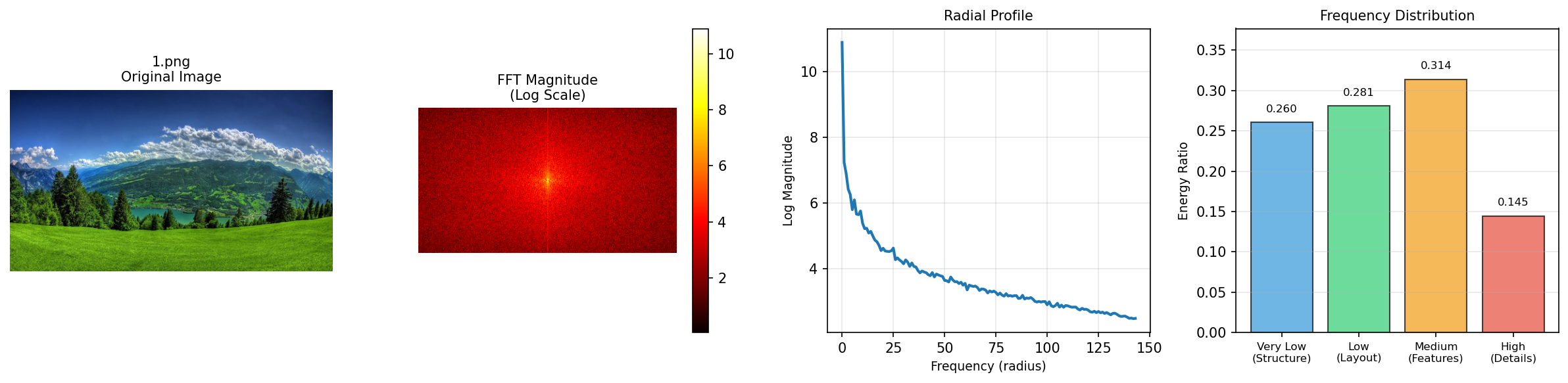
Natural scenery images (landscapes, forests, oceans) are typically rich in intricate, spatially varying details across the entire frame. This leads to:

Relatively low low-frequency energy ratio (few large uniform regions)
High high-frequency energy ratio (abundant textures and details)

Here are some representative examples:

In contrast, side-profile portraits of people usually contain large smooth areas (skin, hair, background) and more localized details. This results in:

Relatively high low-frequency energy ratio
Lower high-frequency energy ratio compared to complex scenery

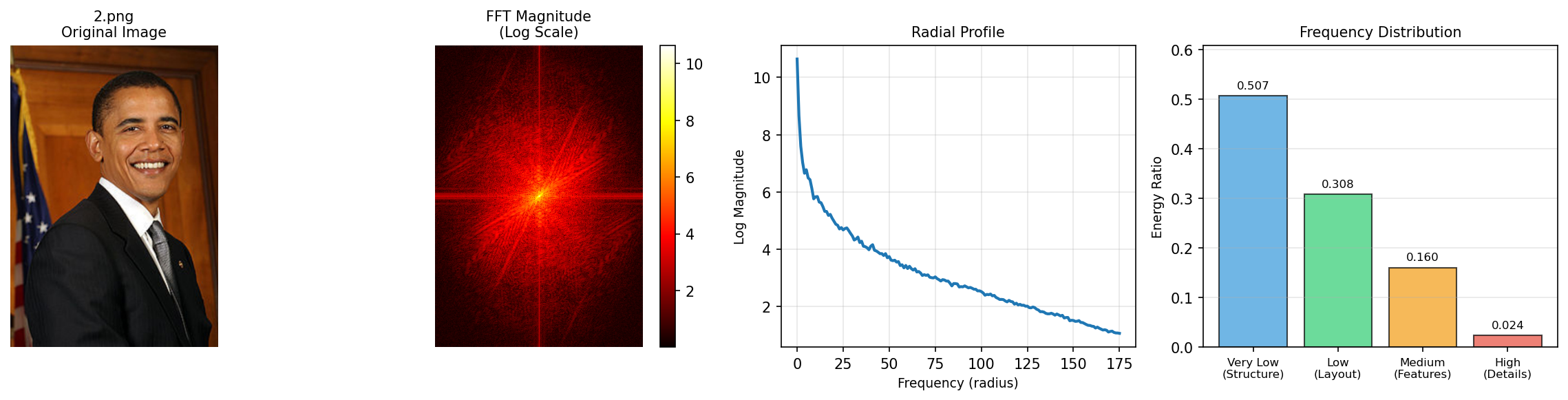
These differences become very clear in their Fourier magnitude spectra (log-scaled for better visualization):

The scenery spectrum is more spread out toward higher frequencies, while the portrait spectrum concentrates energy near the center.

Frequency Evolution in Diffusion Models

Diffusion models generate images by starting from pure Gaussian noise and iteratively denoising over hundreds of steps (the reverse process). A striking pattern emerges when we track frequency content over time:

Low-frequency information (overall layout, major shapes, broad colors) appears and stabilizes relatively early.
High-frequency details (sharp edges, textures, fine patterns) are progressively refined in later steps.

As a result, the ratio of high-frequency energy to low-frequency energy generally increases throughout the denoising process.

Here is a visualization of how the energy of different frequency evovles in diffusion model’s denoising:

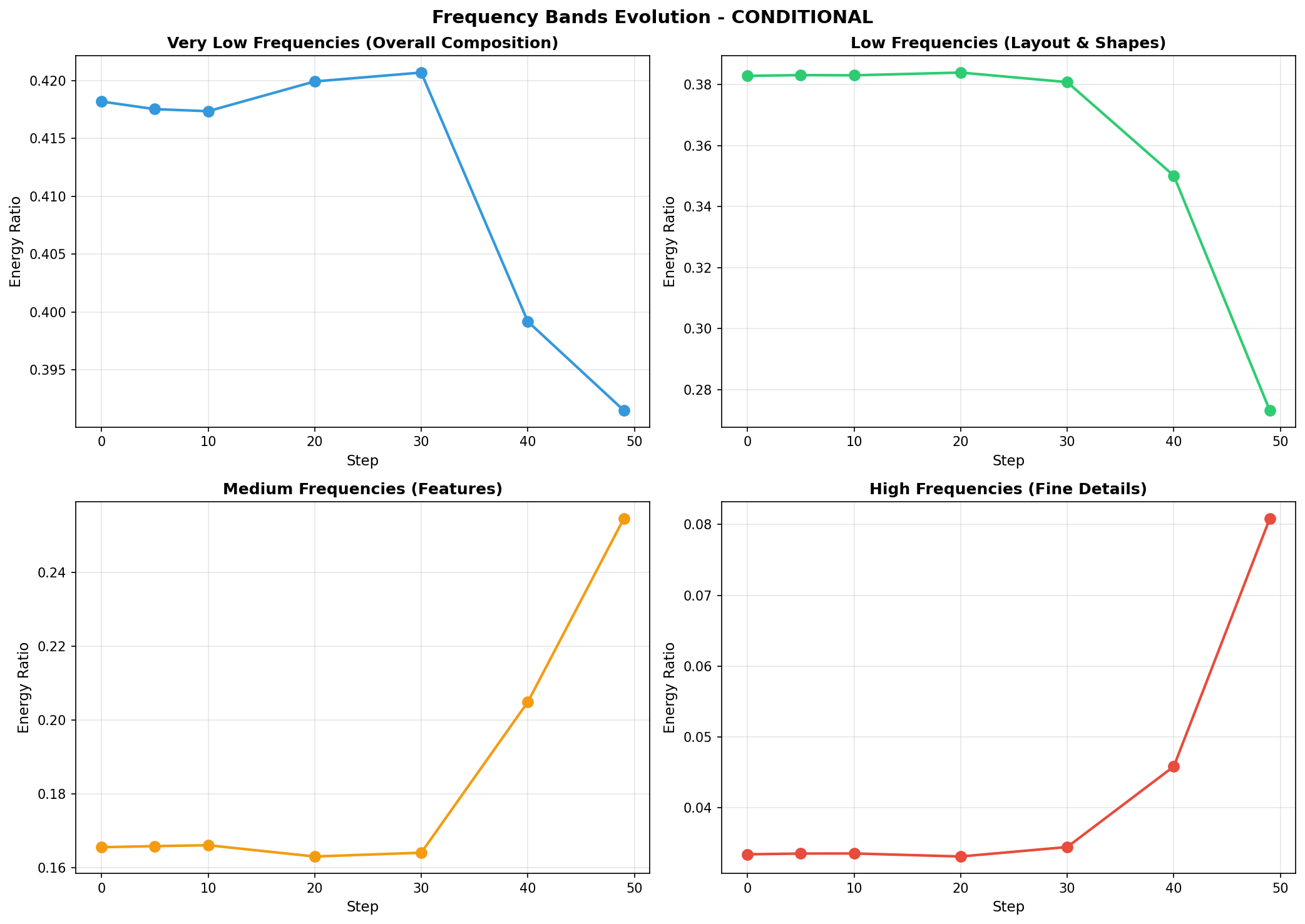
This coarse-to-fine behavior explains much of the success of diffusion models: they first establish “what the image is about” (low frequencies) before adding crisp details (high frequencies). This progression is similar to how humans perceive and draw scenes.

Key Takeaways

Scenery images are richer in high-frequency content due to their detailed textures.
Human portraits have stronger low-frequency content because of smoother regions.
Diffusion models naturally follow a low-to-high frequency progression, which is one reason they produce photorealistic results.

Understanding these frequency dynamics can possibly lead to interesting application: frequency-aware losses, adaptive sampling schedules, or even specialized models for different image domains.