Background

At the beginning of the quarter, advised by my professor, I began to dig deep into this paper: Zeroth-Order Diffusion Monte Carlo (ZOD-MC). The idea is fascinating—a way to sample from tricky distributions without needing them to be log-concave or satisfy fancy inequalities like Log-Sobolev. Also, it uses only zeroth-order queries to the potential V, no gradients. It employs denoising diffusion to handle multimodality and even discontinuities, which is cool for real-world stuff like non-convex potentials with high barriers. I feel like this can be a great starting point for studying and researching sampling and diffusion processes. And I started my journey from here.

2025-11-13

Current stage goal: Implementing partial zod mc on independent distribution.

Progress and work: I have read zodmc, A Proximal Algorithm for Sampling,

But as I read through, the curse of dimensionality hit me hard. The oracle complexity is exp(Õ(d) log(1/ε)), great for low d but very inefficient in high dimensions. In fact, many of the sampling methods it references are either exponential or pseudo-exponential for non-concave functions, or polynomial but concave or with other nice properties. This got me thinking: how to make it better to improve on zero-order sampling? My professor suggested starting with simple cases, like when dimensions are independent or the potential decomposes into lower-dim parts.

That sparked the “partial ZOD-MC” idea. If V(x) breaks into sum V_j(x_j) over b blocks, each of size d/b, I could run ZOD-MC on each block separately. Parallelize it, concatenate samples. Complexity drops to O(b) * exp(Õ(d/b) log(1/ε)). Feels like a win for independent distributions – tested mentally on separable mixtures, seems efficient.

However, implementing the code is quite hard work since the code in the paper only deals with full dimension (log_prob). And no distributions are provided to construct an independent distribution. I need to write log_prob for single dimension and then write custom independent distribution to test my sampling method. After months of efforts, I finally got my method working, and it’s efficient and works perfectly on independent distributions. Which is, although not so significant since it only works on independent distributions, a solid step.

Next, I also tried brainstorming other optimizations, like tweaking the rejection sampling proposal. Maybe a better envelope than Gaussian to boost acceptance. But it doesn’t fit at first. Then, I looked more closely into the paper and found out that the whole thing relies on the OU process and Tweedie’s formula, where the conditional is V plus a quadratic – which is why Gaussian is useful and can’t be replaced. Changing it would mess up the score estimation and guarantees from Theorem 1.

2025-12-25

Is it possible to approximate an arbitrary probability distribution using something like a characteristic function expansion?

I’ve been looking into series expansions that build on the characteristic function to approximate densities. One well-known approach is the Edgeworth expansion, which starts from the standardized normal distribution and adds correction terms based on higher-order cumulants, using Hermite polynomials.

The idea is appealing on paper: it’s a systematic expansion that refines the Central Limit Theorem approximation by incorporating skewness and further moments. In cases where the target distribution is reasonably close to normal, the first few terms can provide useful improvements over the plain normal approximation.

However, after running some numerical experiments, I found that the Edgeworth expansion performs very poorly when the target distribution has separate modes.

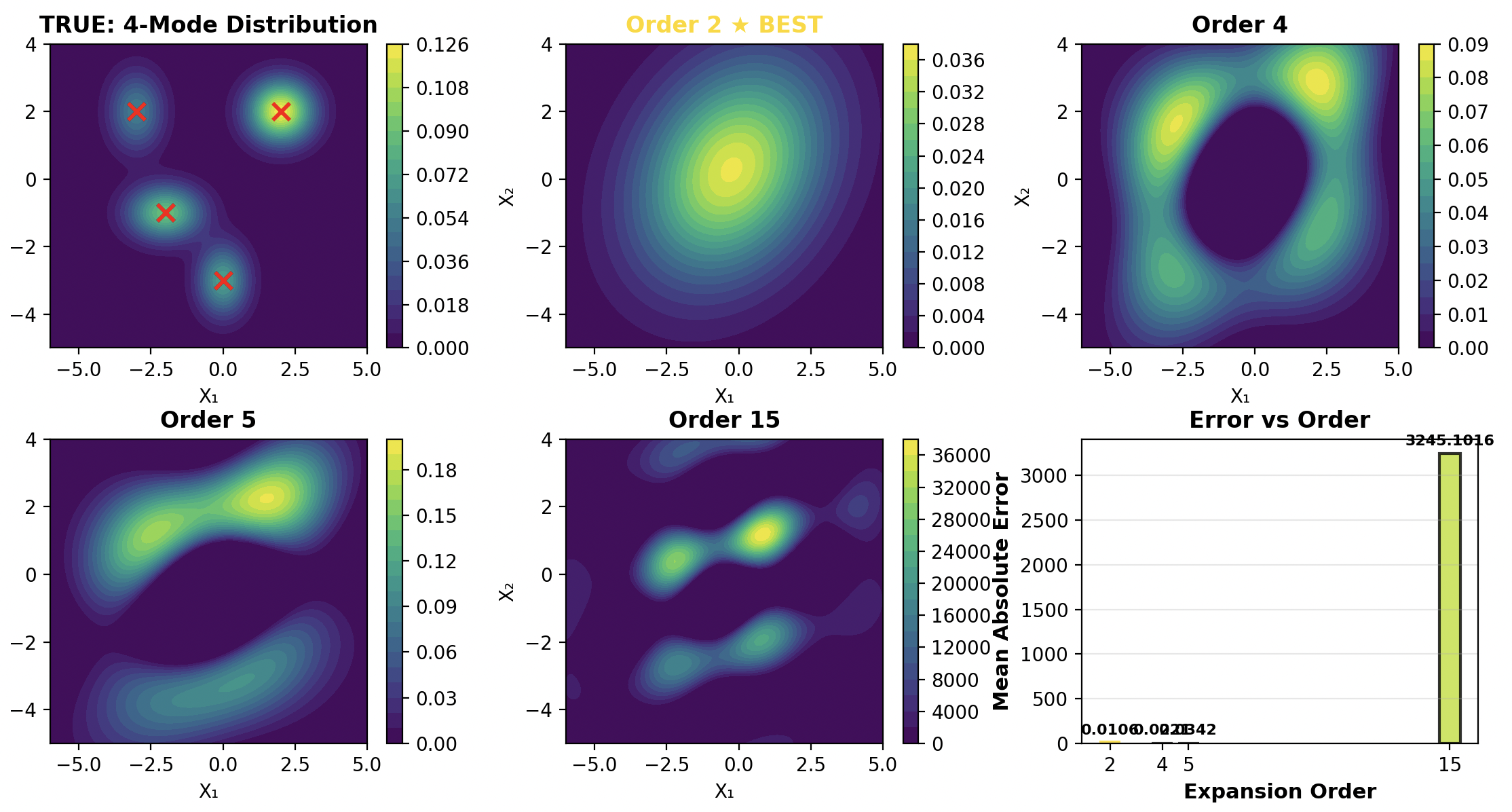
As the figure shows, although the expansion does produce 4 modes, it struggles to capture the four distinct peaks, which indicate that it’s poor at approximate distributions with distinctive modes.

This failure surprises me at first, but after some retrospection, this has some explanations. The Edgeworth series is fundamentally a perturbation around the Gaussian: each additional term is a polynomial correction multiplied by powers of \(\(1/\sqrt{n}\)\) (in the CLT context). When the underlying distribution is far from unimodal or has strong deviations from normality, the series struggles to converge properly and can exhibit pathological behavior like oscillations or non-positive densities.

My tests confirm that these expansions work best for mild departures from normal distribution but are unreliable for multimodal or heavily skewed distributions.

This experience has left me skeptical about using Edgeworth-type expansions for general-purpose density approximation, especially when the shape of the target is unknown or complex. For cases involving distinct modes, other methods will almost certainly be needed.