Background-Positional information

Compared with other sequential model like LSTM and RNN, Transformers are much more successful and serve as the foundation of current language models. These transformer-based LLM achieve higher accuracy than other architecture and can scale up easily due to the parallel computing of Transformer. However, Transformers have its flaws. It requires more computation resources than Sequential model with time complexity of \(O (N^2)\). Also, without external help, Transformers can’t acquire positional information that is important when dealing with sequential data.

What’s positional information? Positional information is about the order of characters appear. For instance, “I eat fish” is different from “Fish eat I” because order of appearance is different. “I” appears first in the first setence and “fish” appears first in the second sentence, resulting each sentence having different meaning.

Transformers can’t acquire the sequential information of words because the way data is passed to the model. For a traditional model like RNN, each data is passed one at a time. For instance, in the sentence “I eat fish,” “I” will be processed first, then “eat”, then “fish.” This way, RNN acquires sequential information of each word.

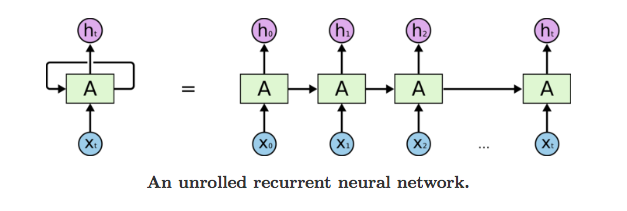
However, for transformers, all words are passed in all at once. The sequential meaning is lost when the model processes data parallelly instead of sequentially. All words in “I eat fish” will be passed into the model at the same time. The model can’t distinquish which words come first, unless we pass in additional positional information about this word.

Of course, we can just simply assign 1, 2, 3, etc to each word position, but researchers found out better ways to encode position of words.

Absolute Positional Encoding - Sinusoidal Positional encoding

Absolute positioinal encoding is first introduced in the paper Attention Is All You Need. It uses trigonometry function, sine and cosine, to encode positions.

For a word \(x\) at position t, the positional encoding will be expressed as:

\[e_t = \begin{bmatrix} sin(w_0 \cdot t) \\ cos(w_0 \cdot t) \\ sin(w_1 \cdot t) \\ cos(w_1 \cdot t) \\ \vdots \\ sin(w_{d/2} \cdot t) \\ cos(w_{d/2} \cdot t) \end{bmatrix} \ \ w_k = \frac{1}{10000^{\frac{2k}{d}}} \ \ where \ \ d \ \ is \ \ the \ \ dimension \ \ of \ \ the \ \ positional \ \ embedding\]

Using trigonometry function has a very good property. Given word \(p_i\) at position i and word \(e_{i+k}\) at position i+k, we can deduce the position between them by taking dot product.

\[\begin{split} e_t \cdot e_{t+k} & = \sum_{i=0}^{\frac{d}{2}-1}sin(w_it)sin(w_i(t+k))+cos(w_it)cos(w_i(t+k)) \\ & = \sum_{i=0}^{\frac{d}{2}-1} cos(w_i(t-(t+k))) \\ & = \sum_{i=0}^{\frac{d}{2}-1} cos(-w_ik) \end{split}\]

We can see that the final result is only dependent on k, the relative distance between each word.

Let’s recall how attention, the main mechanism of Transformer, works with KQV stuffs.

\[Attention(Q,K,V) = softmax(\textbf{QK}^T)\textbf{V}\] \[\textbf{Q} = \textbf{W}_Qx\] \[\textbf{K} = \textbf{W}_Kx\] \[\textbf{V} = \textbf{W}_Vx\]

We may only focus on \(\textbf{QK}^T\) because that’s where two words interact each other. We now inject sinusoidal positional encoding to input vector, so instead of \(x\), it’s \(x+e\). We then calculate attention score for words in position i and j, the result will be:

\(\textbf{W}_Q(x_i+e_i)(\textbf{W}_K(x_j+e_j))^T =\) \(\textbf{W}_Qx_i{x_j}^T\textbf{W}_K+\textbf{W}_Qe_i{x_j}^T\textbf{W}_K+\textbf{W}_Qx_i{e_j}^T\textbf{W}_K+\textbf{W}_Qe_i{e_j}^T\textbf{W}_K\)

We can see that the first term doesn’t contain any positional information of two words. The second and third term only contain positional information of 1 word, which alone can’t deduce the relative positional information. Only the fourth one that has the dot product of two positional embedding contain relative position of two words. This piece of information will be helpful to the model to identify the revelance between each words.

Questions:

1. Why do we add positional embedding to input embedding? What about concatenation? a. It may blur semantic meaning of input embedding by interwining positional embedding with semantic content b. It’ll increase dimension of input vector with no significant increase of model’s accuracy
2. Why many people call sinusoidal positional encoding as absolute? They say it can’t learn relative positional information. a. I searched online looking for answers why this encoding method is absolute and can’t acquire distance between words. Sadly, all the blog I have checked so far didn’t contain detailed mathematical formula to prove it. I guess they call it absolute simply because it only takes the input of current word position and no other word positions.

Rotary Positional Encoding

Conclusion

Positional encoding is one of the most important feature in Transformer. This blog covers one of the encoding method, the Absolute Positional encoding. Many people say about this absolute positional encoding can’t acquire relative distance two words because it’s “absolute.” However, I do some mathematical deduction and show that this encoding method can learn the relative distance between two words. Therefore, it’s useful in acquiring information beside the current position of the word.